In diesem Artikel beschreiben wir, wie sich eine Varianzanalyse (ANOVA) in SPSS berechnen lässt.
Die Daten
Zur Analyse verwenden wir den systeminternen Datensatz contacts.sav. Der Datensatz umfasst diverse Merkmale von N = 100 Unternehmen. Wir wollen die Verkäufe in Abhängigkeit der Unternehmensgröße erklären. Da die Verkäufe metrisch und die Unternehmensgröße nominal ist, bietet sich eine VArianzanalyse zur Untersuchhung an.
Die Analyse
Um eine Varianzanalyse in SPSS durchzuführen gehen Sie aud Analysieren > Mittelwert und Proportionen vergleichen > Einfaktorielle Varianzanalyse.
Daraufhin öffnet sich das folgende Dialogfeld.
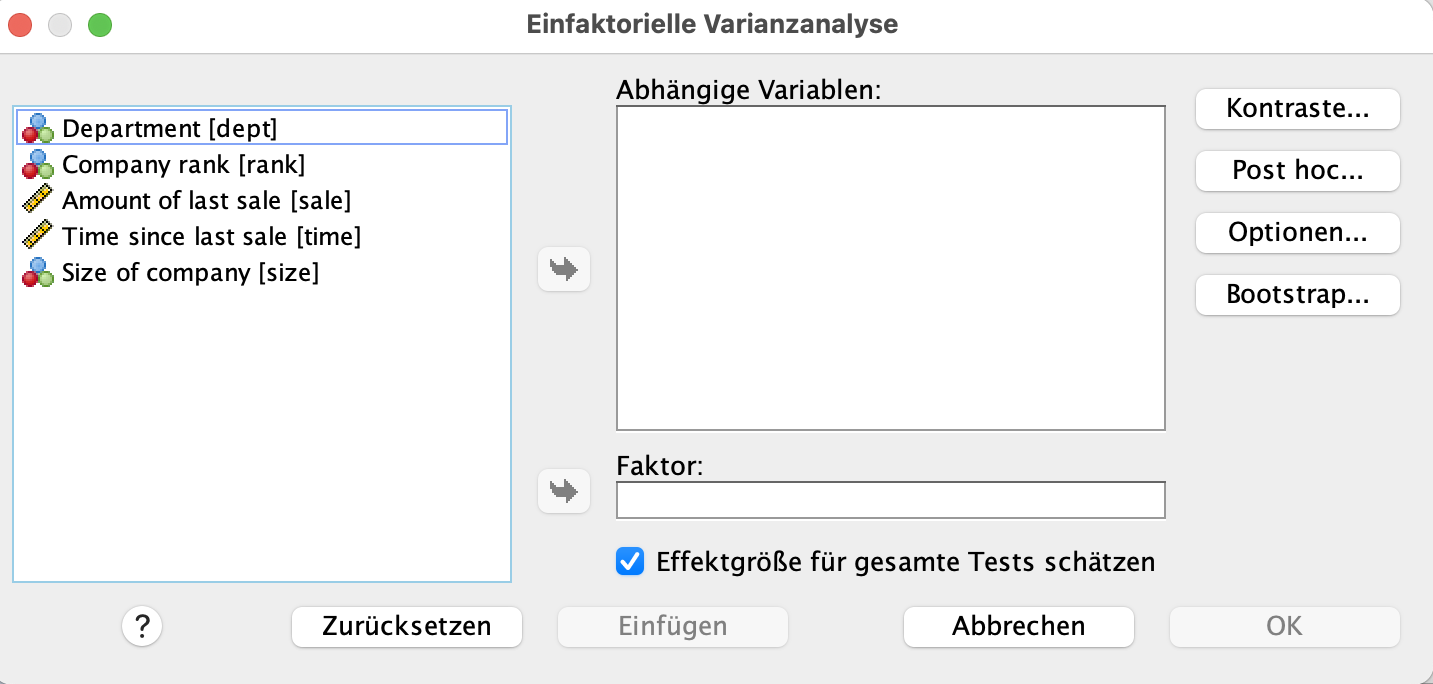
Die abhängige Variable ist hierbei die Verkäufe. Fügen Sie die Variable sale als in das Feld Abhänigge Variablen. Wir wollen die Verkäufe in Abhängigkeit der Unternehmensgröße untersuchen. Somit ist die Variable size unsere unabhängige Variable, im Kontext zur ANOVA wird die unabhänbgige Variable auch häufig Faktor genannt. Fügen Sie also die Variable size in das Feld Faktor ein. Das Dialogfeld sollte nun, wie folgt aussehen.
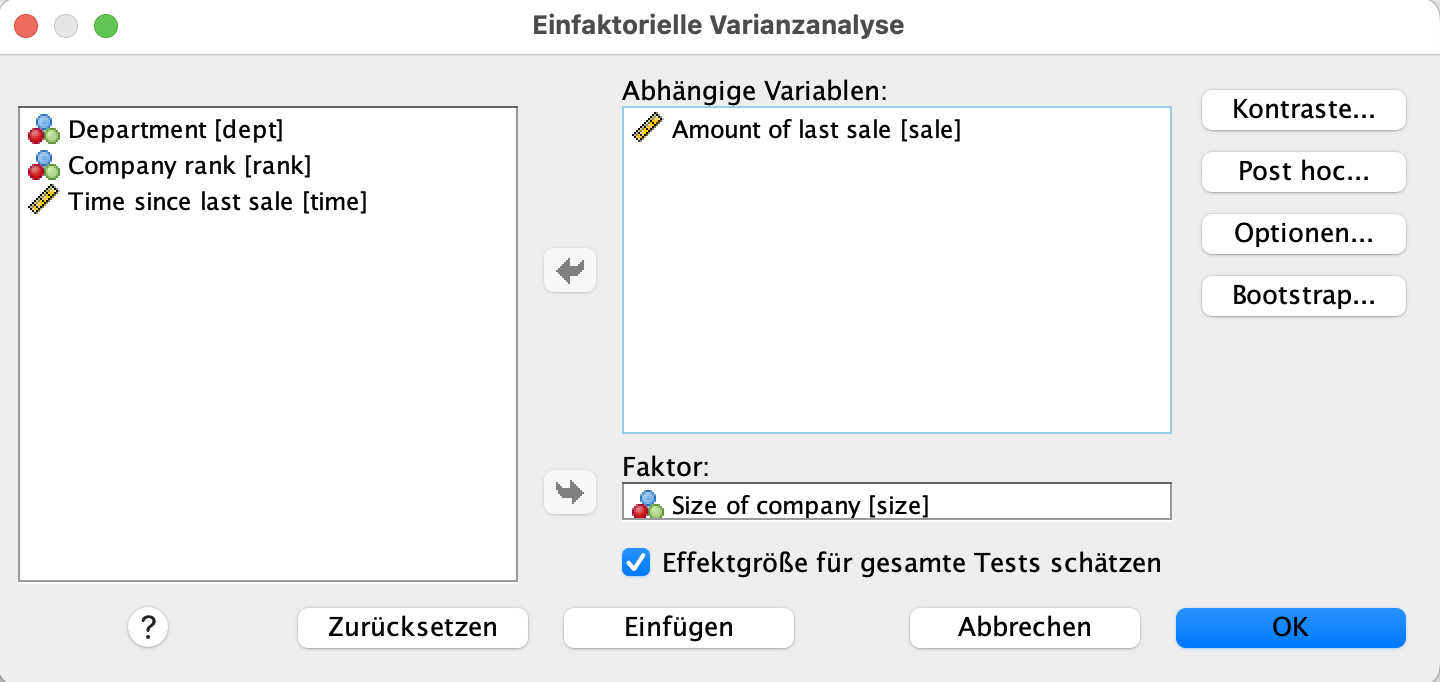
Nun drücken Sie auf Post hoc. Es öffnet sich das kommende Fenster.
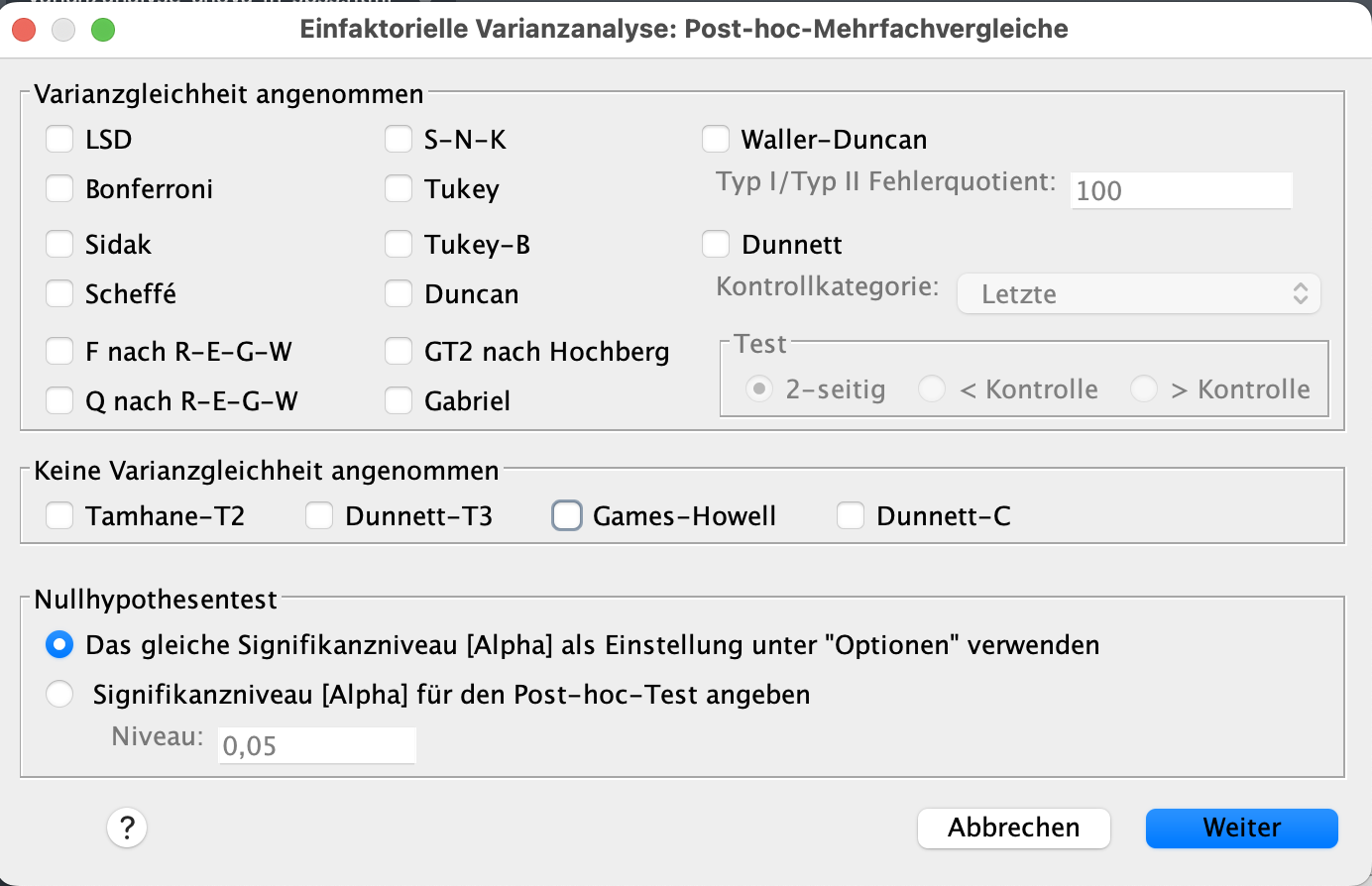
Post Hoc Tests dienen zur Prüfung, welche Faktorausprägungen, in unserem Falle Unternehmensgrößen, sich signifikant unterscheiden. Die Durchführung eines Post Hoc Tests stetzt dabei ein signifikanter Haupteffekt in der ANOVA voraus. Es gibt für zwei Varianten hierbei Post hoc Test. Falls Varianzgleichheit oder Varianzungleichheit zwischen den Faktorstufen vorliegt. Da noch nicht bekannt ist, ob Gleichheit oder Ungleichheit der Varianzen vorliegt, wählen wir jeweils einen Post hoc Test an. Setzen Sie hier jeweils einen Haken bei Tuckey und Games-Howell, sodass das Fenster, wie folgt aussieht.
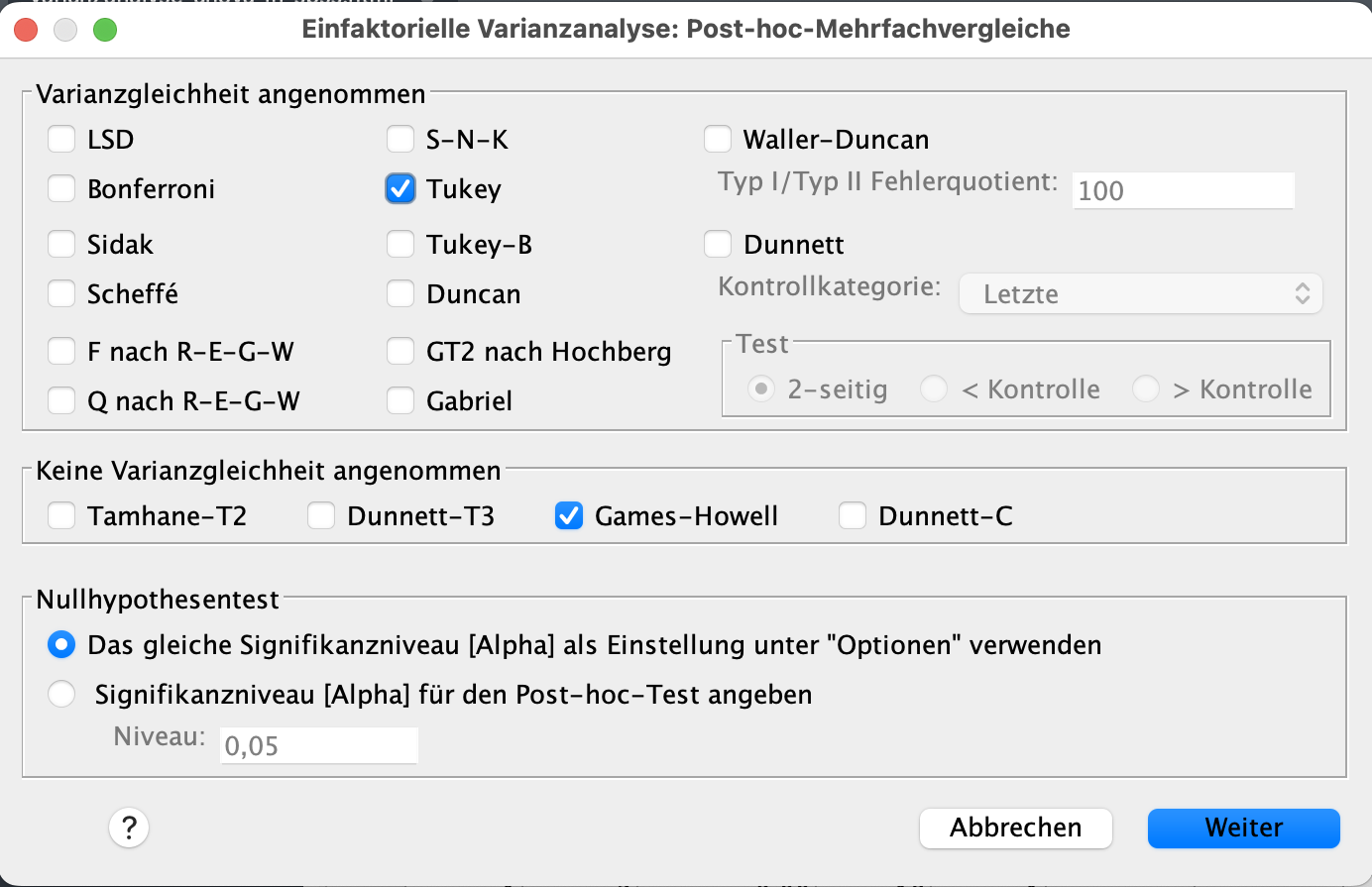
Drücken Sie nun auf Weiter. Wir befinden uns nun wieder im Hauptdialogfeld zur Varianzanalyse.
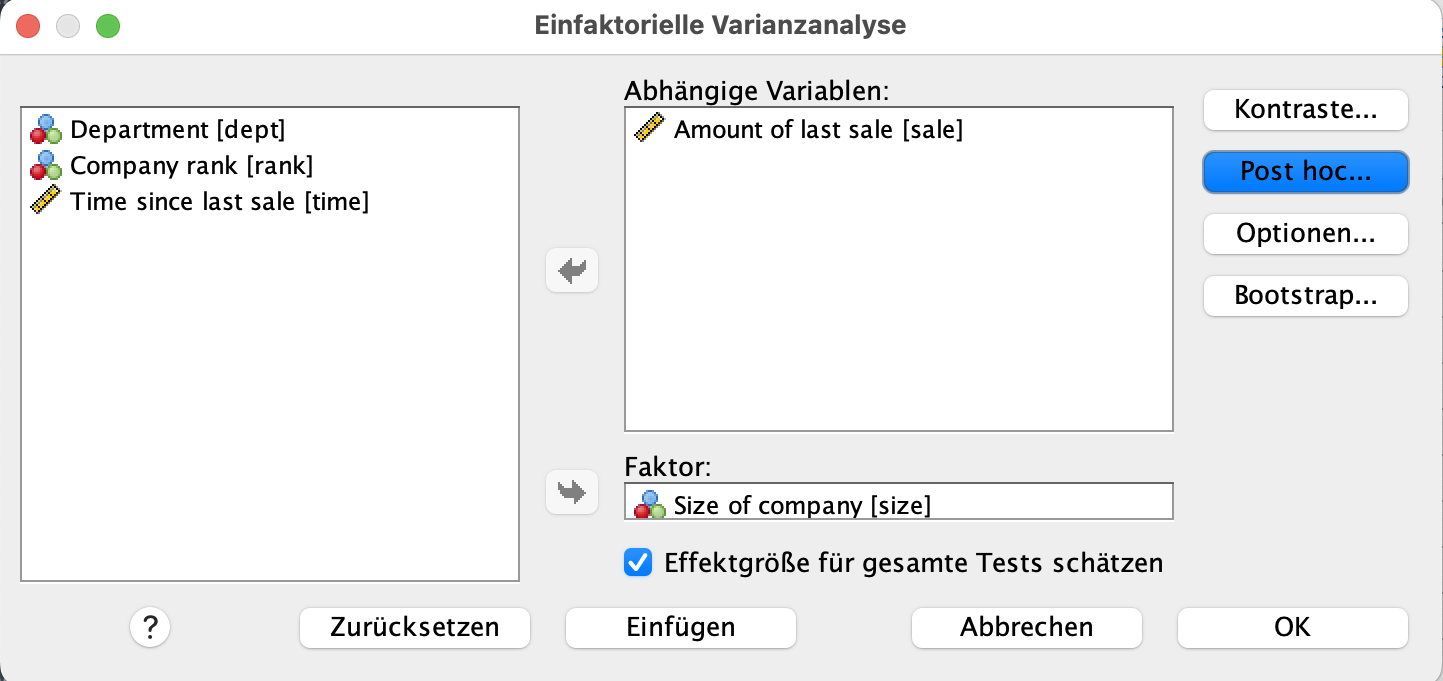
Hier drücken nun auf Optionen. Es öffnet sich das kommende Dialogfeld. Setzen sie hierbei jeweils einen Haken bei Test auf Deskriptive Statistiken, Homogenität der Varianzen und Welch-Test.
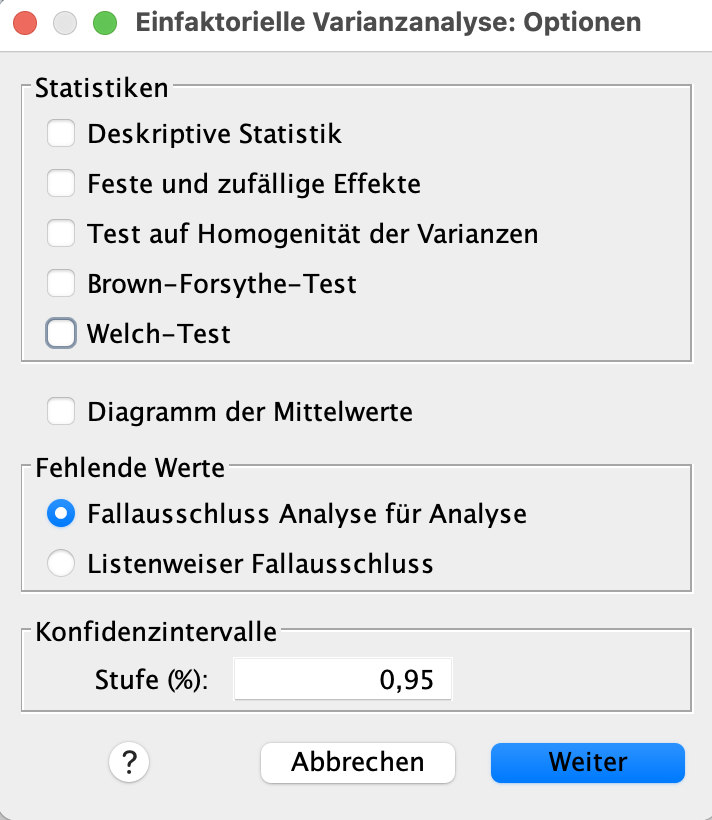
Das Dialogfeld sieht nun wie folgt aus. Nun drücken Sie auf Weiter.
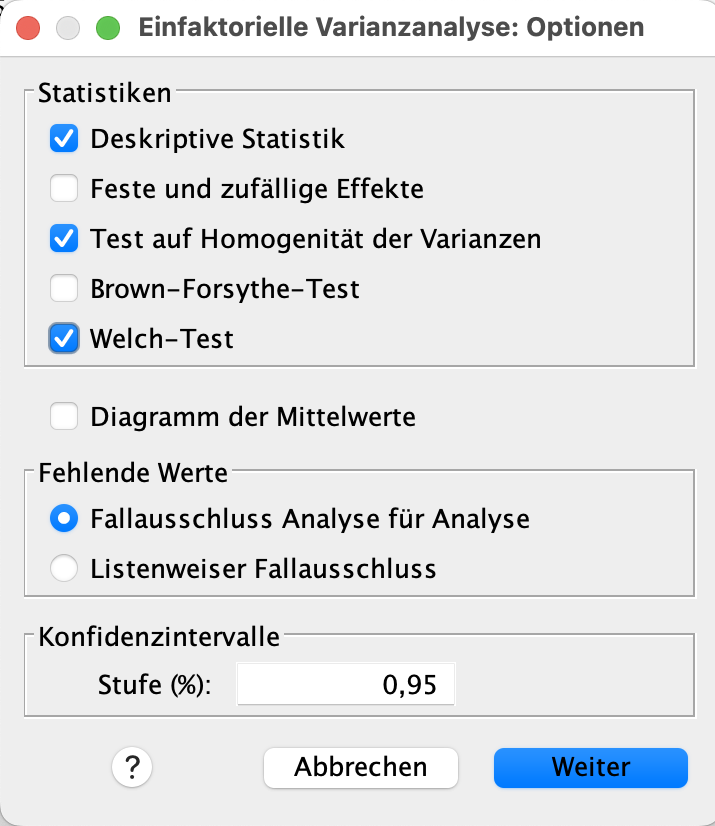
Sie befinden sich nun wieder im Hauptdialogfeld der ANOVA. Nun drücken Sie auf OK. Es erscheinen nun einige Tabellen in der SPSS-Ausgabe.
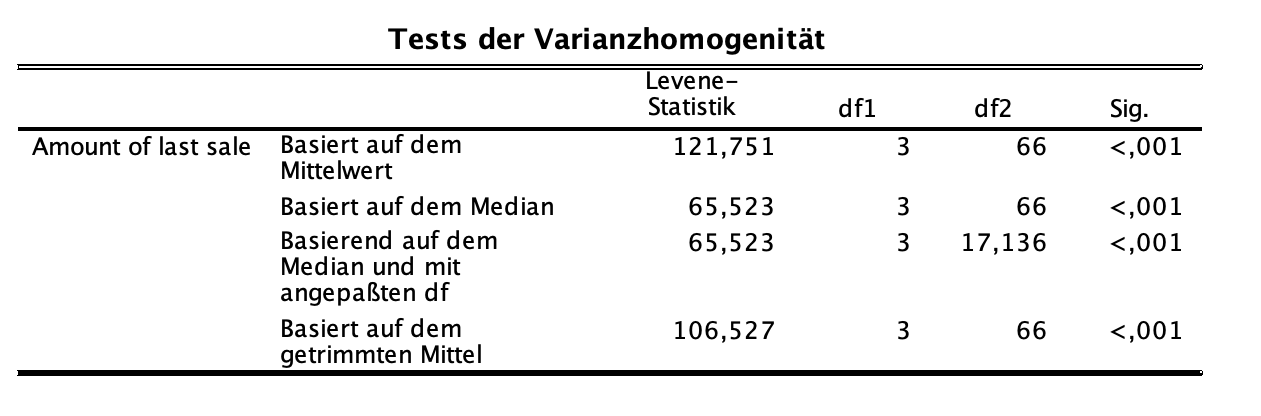
Wir werden hier nur die wichtigsten Tabellen behandeln und erläutern. Zunächst ist das die Tabelle Tests der Varianzhomogenität. Die Gleichheit der Varianzen zwischen den Faktorstufen wird mittels des Levene-Tests überprüft. Hierbei gibt SPSS vier verschiedene Varianten des Tests aus. Die klassische Variante des Levene-Tests ist in der ersten Zeile der Tabelle angegeben. Hier zeigt sich, dass die Varianzen signifikant unterschiedlcih sind, F(3, 66) = 121,75, p = 0,000. Es liegt also eine Verletzung der Varianzhomogenität vor. Somit muss der Haupteffekt Unternehmensgröße mittels des Welch-Tests auf Unterschiede untersucht werden. Wir werden also nicht die Tabelle ANOVA nutzen um das Ergebnis zu interpretieren. Die Tabelle mit der Überschrift ANOVA würden wir nutzen bei Varianzgleichheit. In unserem Falle wenden wir den Welch-Test an, da Varianzungleichheit vorliegt.
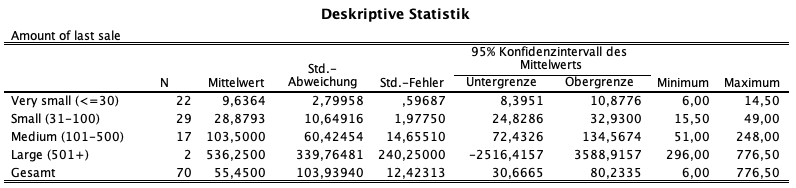
Weiterhin ist es interessant, sich die deskriptiven Statistiken anzuschauen. Es zeigt sich, dass mit steigender Unternehmensgröße auch die Verkaufszahlen höher werden. Weiterhin fällt auf, dass die Kategorie Large jedoch nur mit 2 Beobachtungen besetzt ist.
Die nächste Tabelle zeigt das Ergebnis des Welch-Tests. Hierbei zeigt sich, dass der Welch-Test ein signifikantes Ergebnis liefert, F(3, 4,58) = 33,85, p = 0,001. Somit liegen signifikante Unterschiede in den Verkäufen zwischen den verschiedenen Unternehmensgrößen vor.

Da der Haupteffekt signifikantist, werden gleich Post hoch Analysen, wegen der Varianzungleichheit nach Games-Howell, durchgeführt. Zuvor wird jedoch der Effekt zwischen den Unternehmensgrößen in seinem Ausmaß beurteilt. Hierfür nutzen wir das partielle eta Quadrat. Fautregeln nach Cohen sind hierbei eta größer 0,01 ist ein kleiner, eta größer 0,06 ist ein mittelstarker und eta größer 0,14 ist ein starker Effekt.

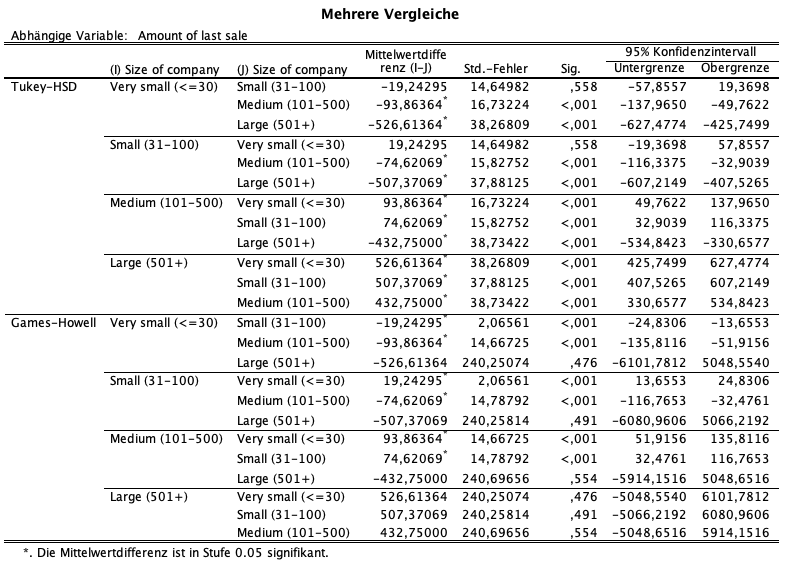
Kommende Tabelle zeigt die Ergebnisse der Post hoc Tests. Wir orientieren uns an den unteren Teil der Tabelle. Hier stehen die Ergebnisse des Tests nahc Games-Howell. Diesen nutzen wir wegen der verletzten Varianzhomogenität. Es zeigen sich hierbei zwischen very small und small, wie auch zwischen very small und medium signifikante Unterschiede, jeweils p = 0,000. Zwischen very small und large zeigten sich keine signifikanten Unterschiede, p = 0,476. Weiterhin unterscheiden sich small und medium signfikant, p = 0,000. Zwischen small und large zeigten sich keine signifikante Unterschiede, p = 0,491. Ebenfalls unterscheiden sich medium und large nicht-signifikant, p = 0,554. Der Grund weswegen sich large zu keiner der anderen Faktorstufen signifikant unterscheidet, trotz der deskriptiv deutlichen Unterschiede, ist in der geringen Stichprobengröße von large begründet.
Derzeit haben wir nur die Annahme der Varianzhomogenität überprüft. Sie müssen also noch die Normalverteilung überprüfen. Hierzu benötigen wir die Residuen der ANOVA. Bei der genutzten Menu können wir uns jedoch die Residuen nicht als Variablen abspeichern. Gehen Sie hierzu auf Analysieren > allgemeines lineares Modell > Univariate.
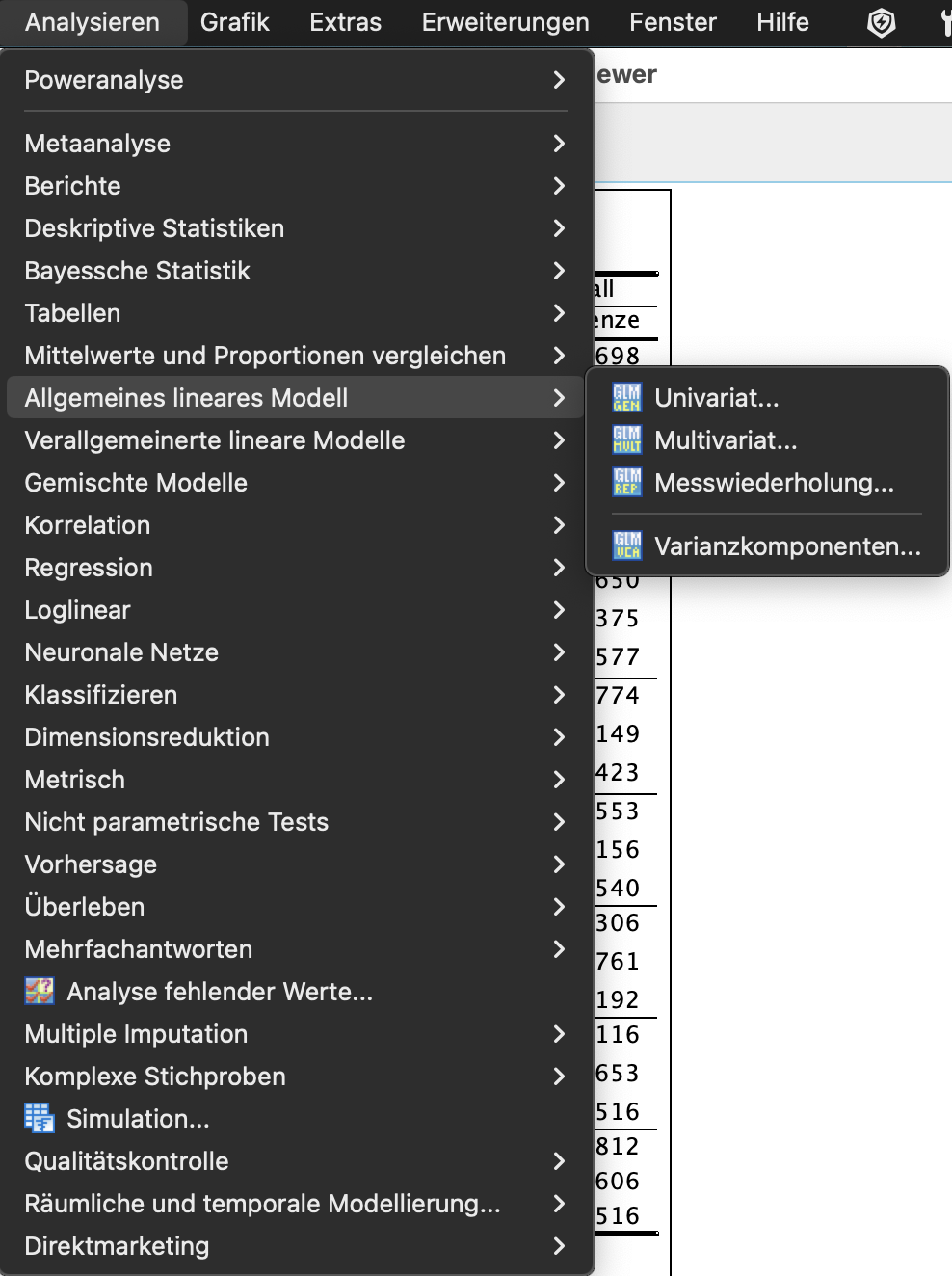
Es öffnet sich das kommende Menü.
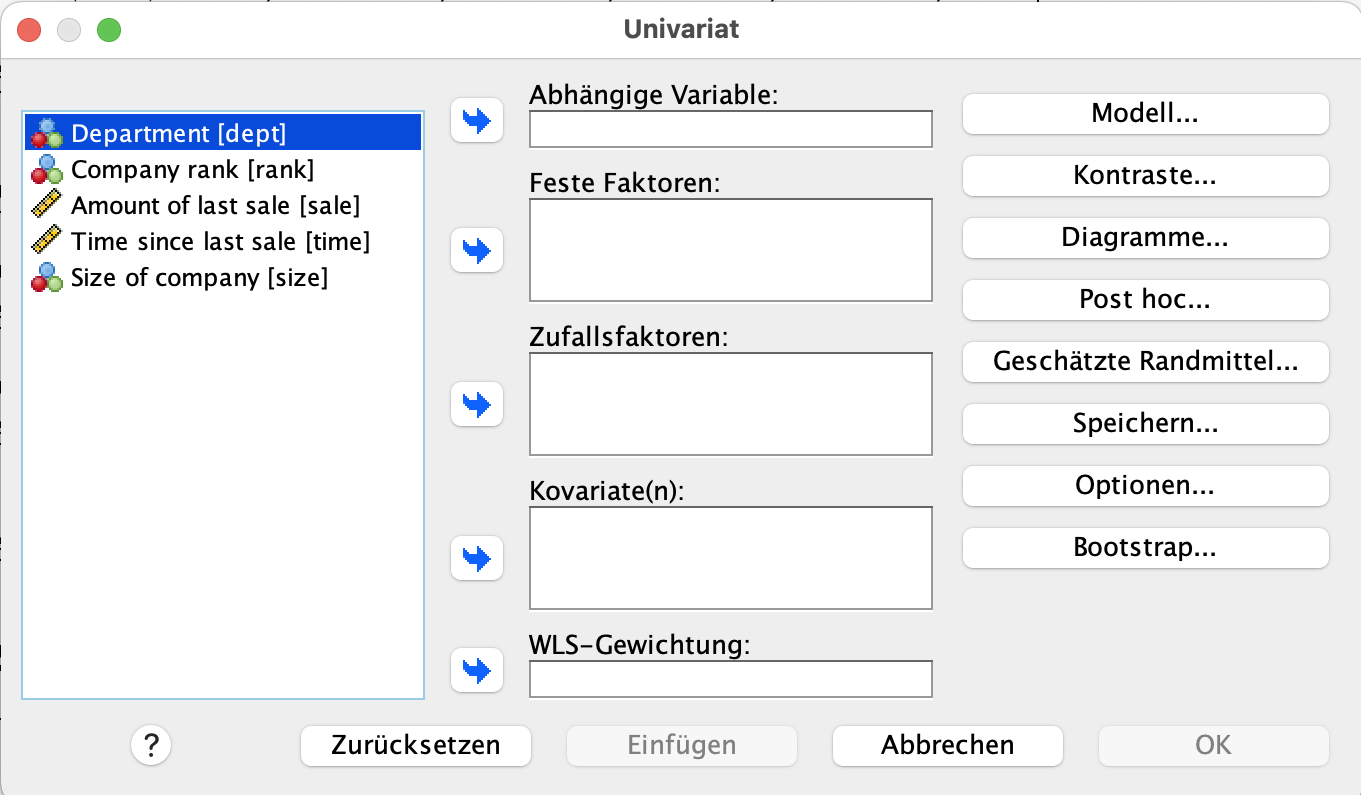
Hier fügen wir die Variable Sale in das Feld abhängige Variable und size in das Feld feste Faktoren. Das Dialogfeld sind nun so aus.
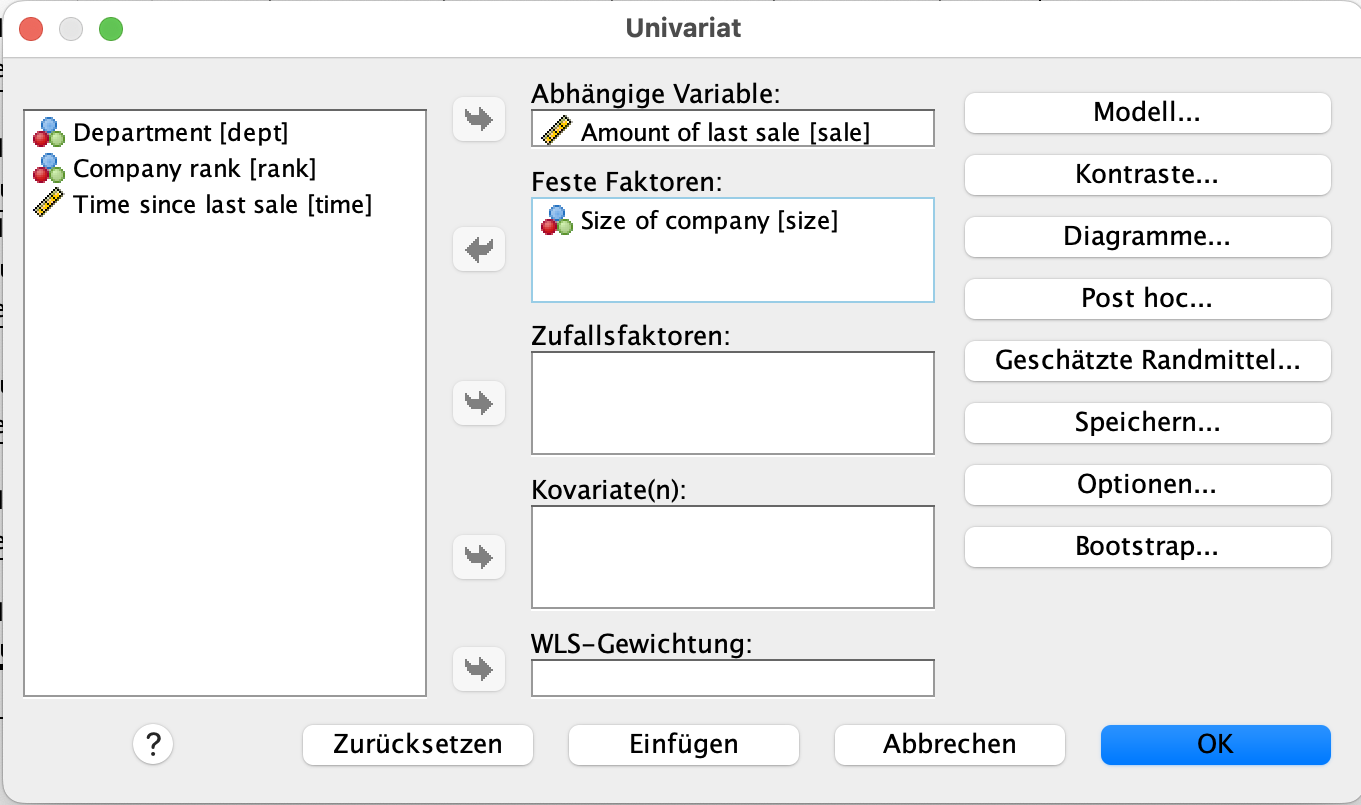
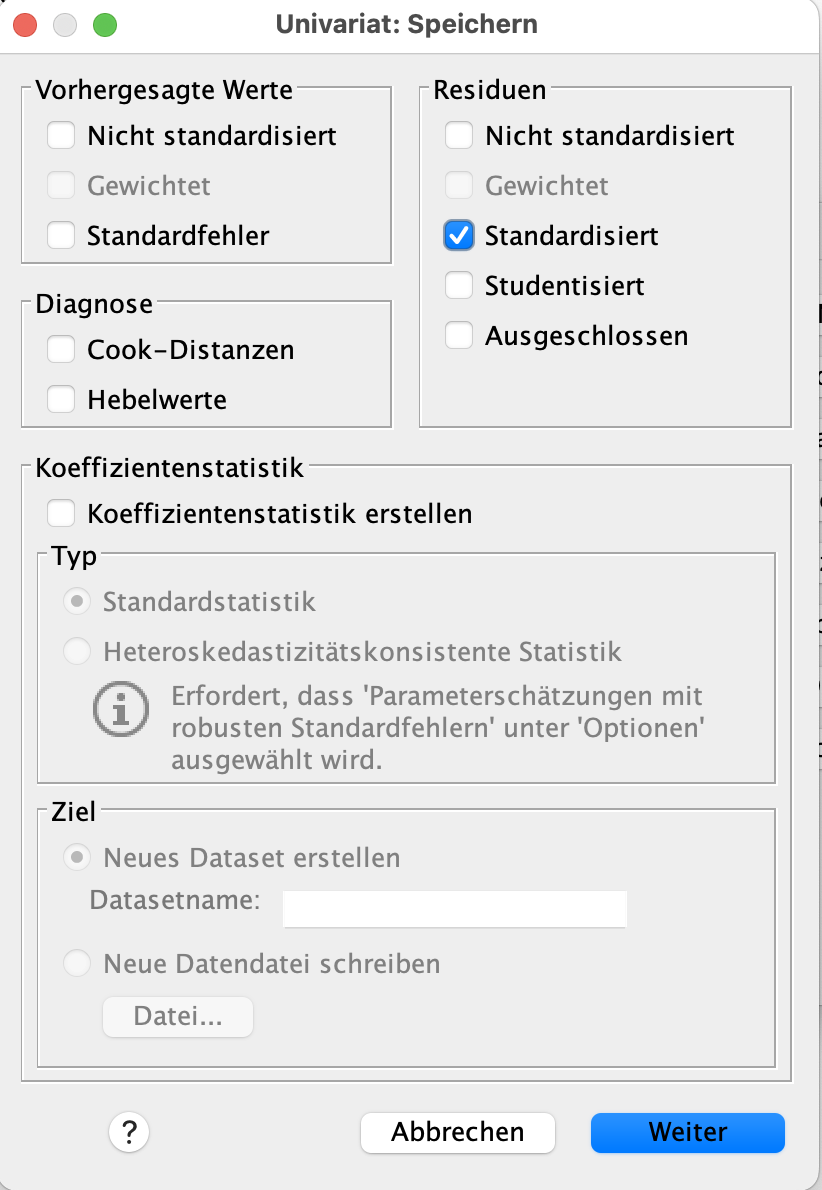
Nun drücken wir auf Speichern. Es öffnet sich das kommende Fenster.
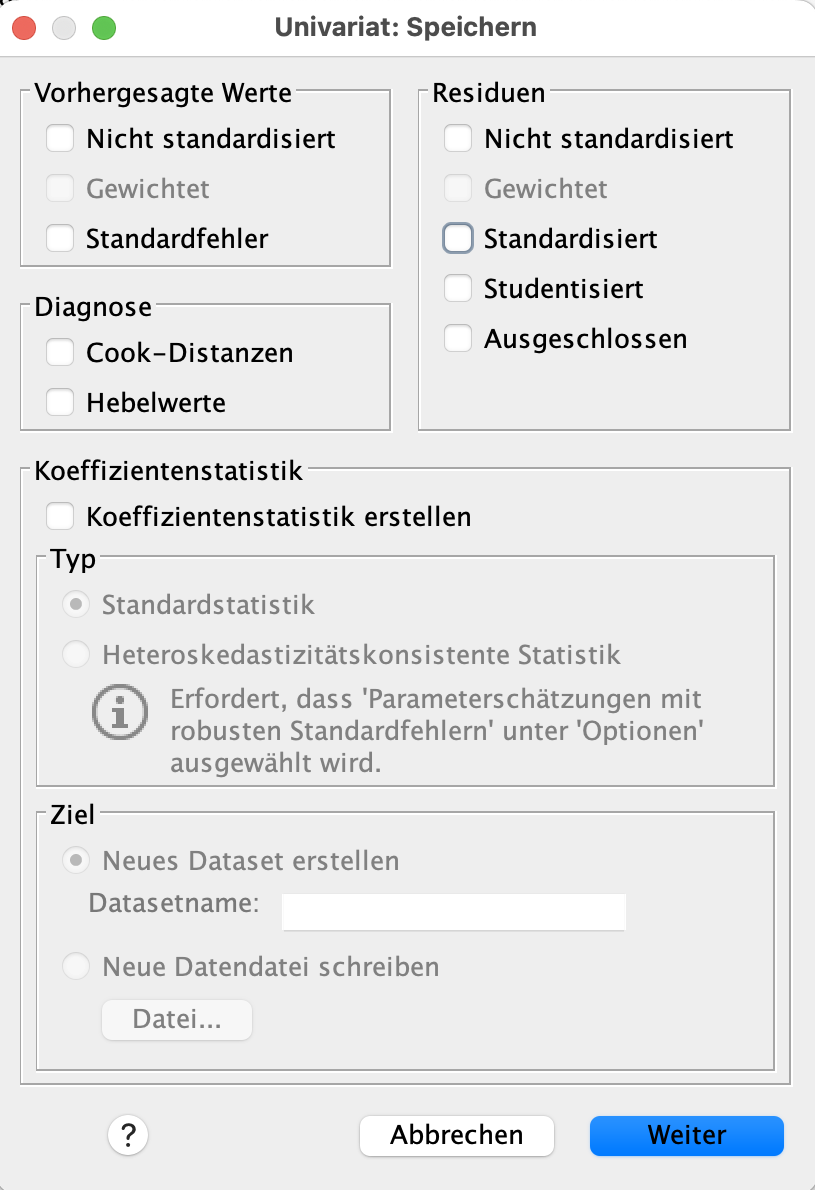
Hier setzen wir einen Haken bei Residuen > Standardisiert. Das Feld sieht nun so aus. Jetzt drücken wir auf Weiter.
Nun befinden wir uns im Hauptmenu des allgemeinen linearen Modells. Hier drücken wir auf OK.

Es befindet sich nun eine neue Variable im Datensatz ZRE_1. Hierbei handelt es sich um die standardisierten Residuen.
Wir gehen nun auf Analysieren > Deskriptive Statistik > Explorative Datenanalyse.
Es öffent sich das kommende Menu.
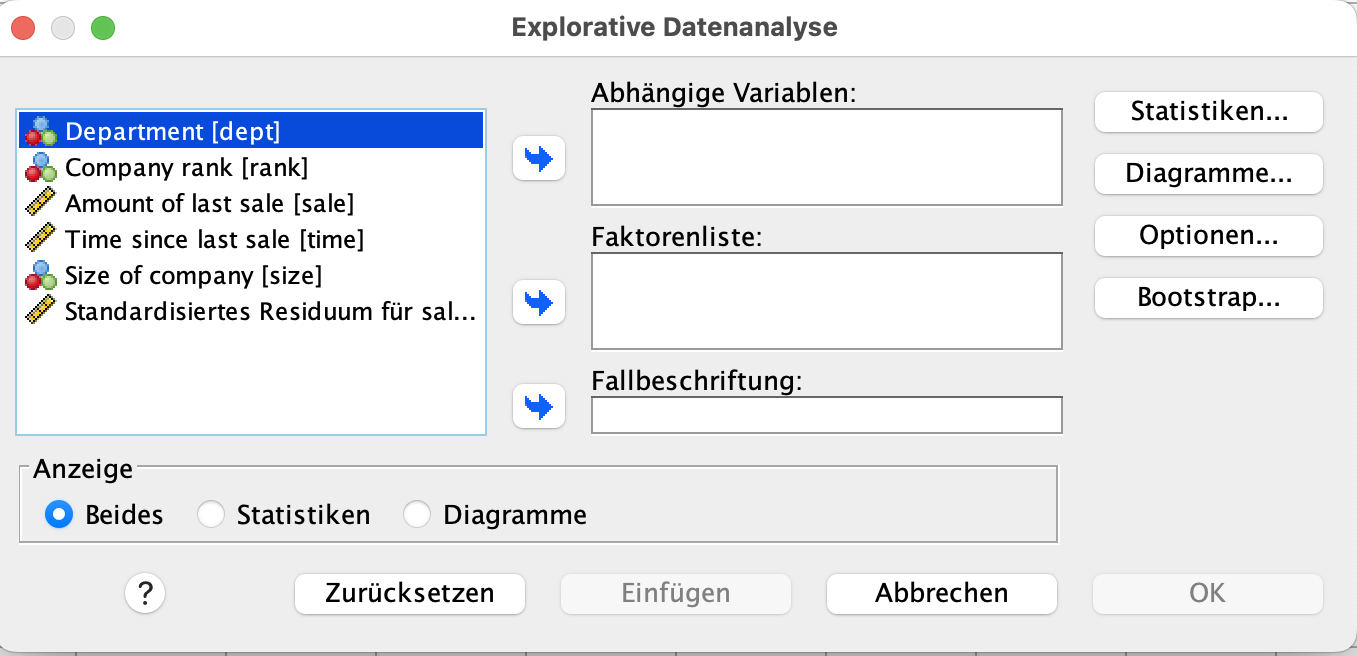
In das Feld abhängige Variable fügen Sie hierbei ZRE_1 ein. Weiterhin drücken wir bei Anzeige Diagramme. Das Dialogfeld sieht nun so aus.
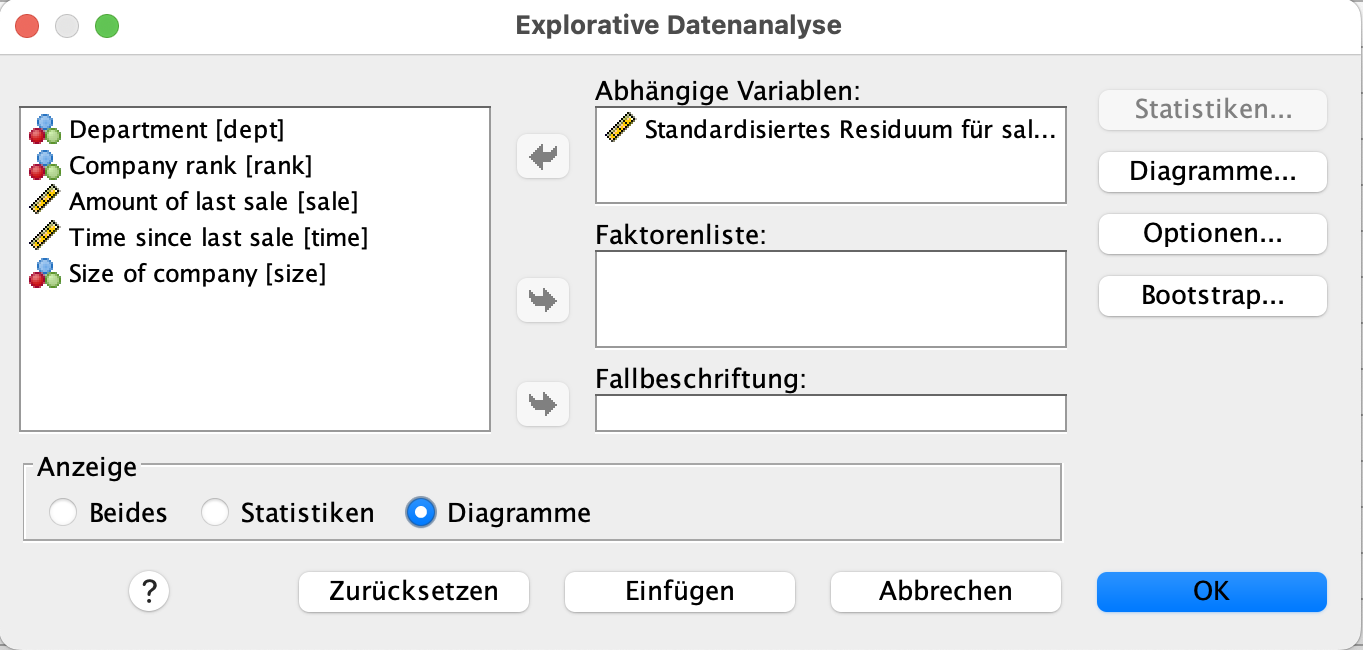
Nun drücken Sie auf Diagramme. Es öffnet sich ein weiteres Fenster.
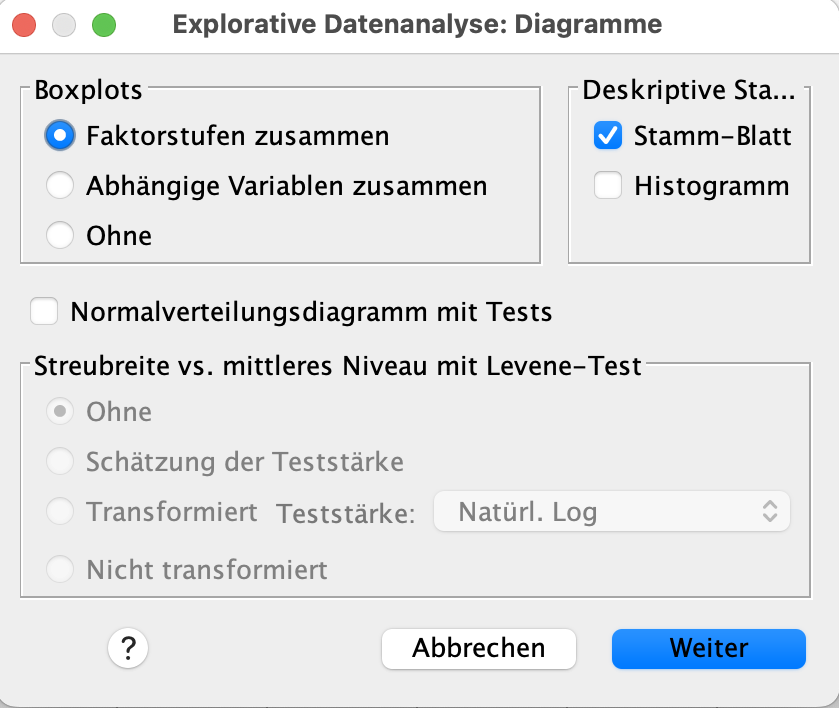
Bei Boxplots klicken wir auf ohne. Weiterhin machen wir den Haken bei Stamm-Blatt weg. Dafür setzen wir den Haken bei Normalverteilungsdiagramm mit Tests. Das Fenstern sieht nun so aus. Jetzt drücken wir auf Weiter.
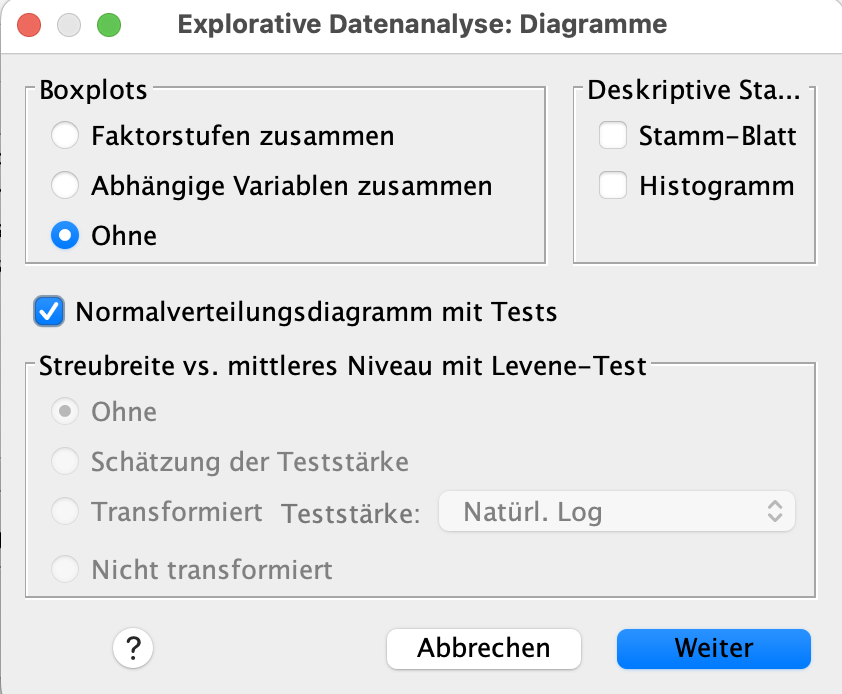
Wir befinden uns nun wieder im Hauptmenu der explorativen Datenanalyse. Hier drücken wir auf OK.

In der Ausgabe erscheinen nun Grafiken und Tabellen. Wir stellen nun das gewöhnliche Q-Q-Diagramm dar.
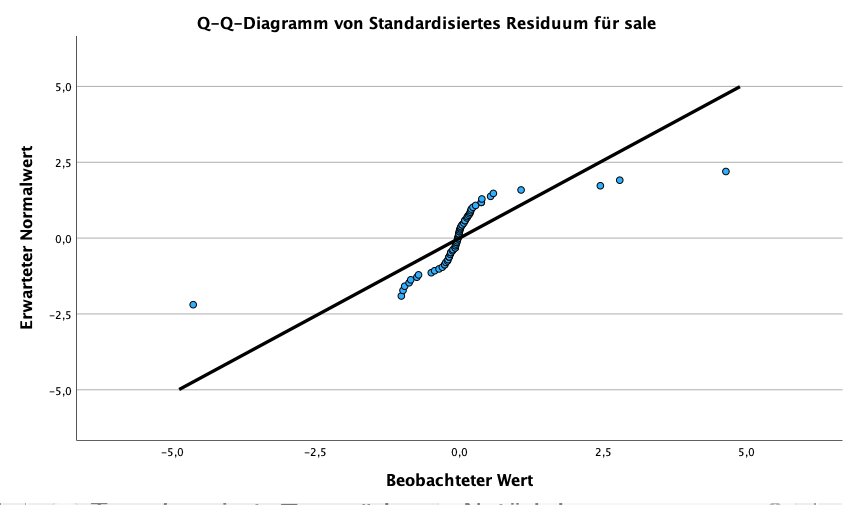
Die Daten scheinen nicht einer Normalverteilung zu folgen. In dieser Situation können Sie die Varianzanalyse mittels eines Bootstraps durchführen. Alternativ können Sie auch den nicht-parametrischen Kruskal-Wallis-Test nutzen.
Sie interessieren sich für Analysen in SPSS. Dann besuchen Sie unsere SPSS-Hilfe.
