Q-Q-Plot (Quantile-Quantile-Plot): Eine umfassende Einführung

1. Einführung: Was ist ein Q-Q-Plot?

Ein Q-Q-Plot (Quantile-Quantile-Plot) ist ein statistisches Werkzeug zur Visualisierung, das verwendet wird, um zu beurteilen, ob eine Datensatzverteilung einer theoretischen Verteilung, wie z. B. einer Normalverteilung, entspricht. Dabei werden die Quantile einer empirischen Verteilung gegen die Quantile einer theoretischen Verteilung aufgetragen.

Definitionen:

• Quantil: Ein Punkt, der eine Verteilung in Teile teilt, z. B. das 50%-Quantil (Median).
• Q-Q-Plot: Ein Diagramm, das empirische gegen theoretische Quantile aufträgt.

Anwendungsbereiche:

• Überprüfung der Normalverteilung für Hypothesentests.
• Analyse von Residuen in Regressionsmodellen.
• Identifizierung von Ausreißern in Daten.
• Validierung statistischer Annahmen.

2. Wie funktioniert ein Q-Q-Plot?

1. Daten sammeln und sortieren: Die Daten werden aufsteigend sortiert.
2. Quantile berechnen: Empirische Quantile der Stichprobe berechnen.
3. Theoretische Quantile ermitteln: Die Quantile einer theoretischen Verteilung berechnen.
4. Punkte plotten: Die empirischen gegen die theoretischen Quantile auftragen.
5. Interpretation: Liegen die Punkte entlang der Diagonalen, folgt die Stichprobe der theoretischen Verteilung.

3. Interpretation eines Q-Q-Plots

Die Interpretation eines Q-Q-Plots erfolgt anhand der Ausrichtung der Punkte zur Diagonalen:

• Linie entlang der Diagonalen: Die Daten sind gut an die theoretische Verteilung angepasst.
• S-förmige Abweichung: Hinweise auf positive oder negative Schiefe.
• Gekrümmte Form: Deutet auf dickere oder dünnere Ränder hin.
• Ausreißer: Einzelne Punkte, die weit von der Linie entfernt sind, weisen auf Ausreißer hin.

4. Exemplarischer Q-Q-Plot

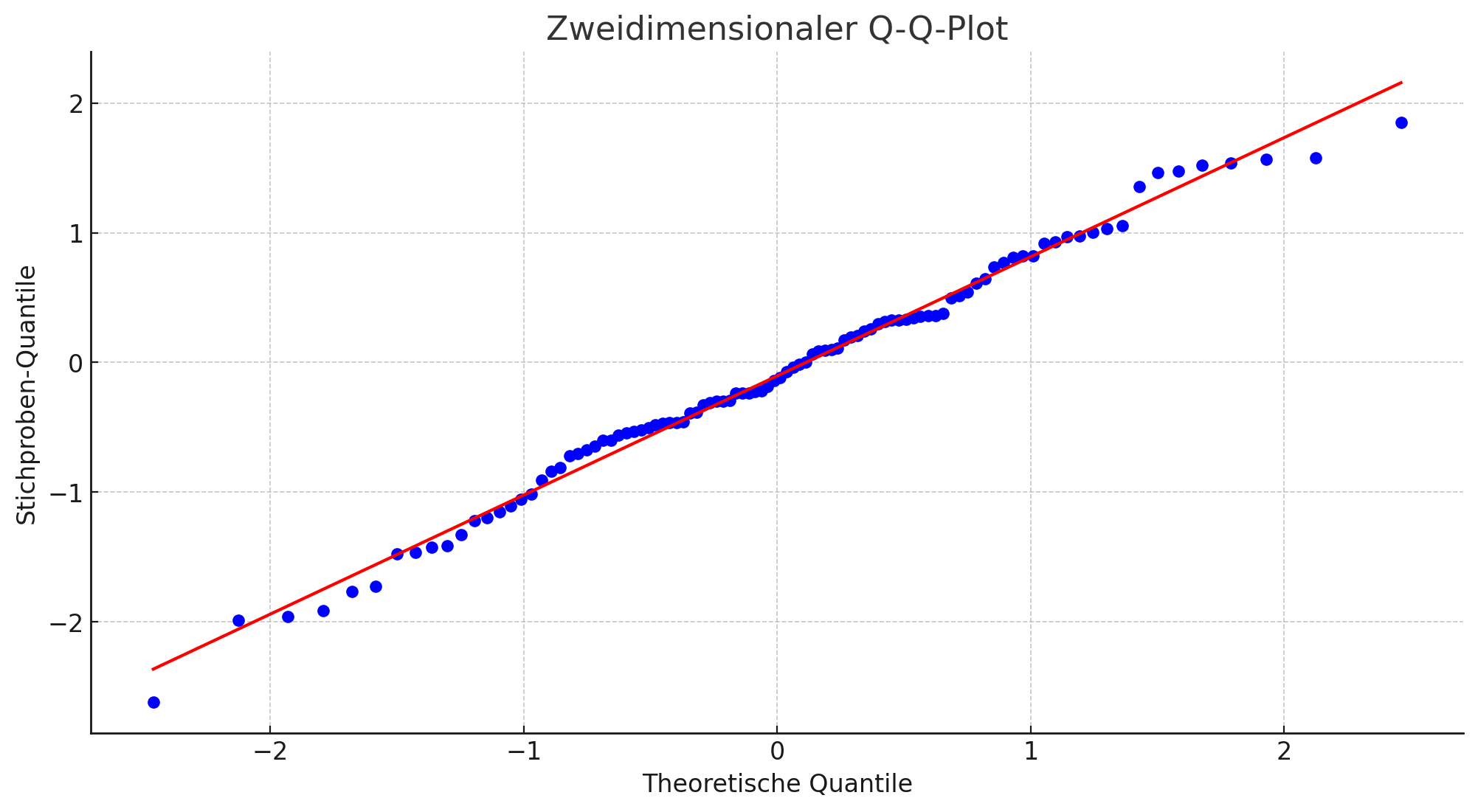
5. Umsetzung eines Q-Q-Plots in verschiedenen Software-Systemen

5.1 R

# Beispiel in R
set.seed(42)
data <- rnorm(100)
qqnorm(data)
qqline(data, col = "red")

5.2 Python

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

np.random.seed(42)
data = np.random.normal(loc=0, scale=1, size=100)
stats.probplot(data, dist="norm", plot=plt)
plt.title("Q-Q-Plot in Python")
plt.grid(True)
plt.show()

5.3 Stata

// Beispiel in Stata
clear
set seed 42
set obs 100
gen data = rnormal()
qnorm data

5.4 SPSS

In SPSS kannst du einen Q-Q-Plot über die Benutzeroberfläche erstellen:

• Gehe zu Analyze > Descriptive Statistics > Q-Q Plots.

5.5 JASP

In JASP wird der Q-Q-Plot über Descriptives und die Option Q-Q Plots generiert.

6. Anwendungsfälle für Q-Q-Plots

• Medizinische Studien: Überprüfung der Normalverteilung klinischer Daten.
• Finanzanalyse: Analyse von Renditen zur Bewertung von Modellen.
• Maschinelles Lernen: Überprüfung der Residuen in Regressionsmodellen.
• Qualitätskontrolle: Identifizierung von Abweichungen in Produktionsprozessen.

7. Erweiterungsmöglichkeiten für den Inhalt

• Mathematische Grundlagen: Erklärung der Berechnung von Quantilen und Normalverteilungen.
• Vergleich mit Alternativen: P-P-Plots, Violinplots und Density Plots.
• Interaktive Q-Q-Plots: Erstellen interaktiver Diagramme mit Plotly.
• Fortgeschrittene Residuenanalyse: Überprüfung von Modellannahmen in der linearen Regression.

8. Fazit

Der Q-Q-Plot ist ein wertvolles Werkzeug zur Überprüfung der Verteilung von Daten und hilft dabei, statistische Annahmen zu validieren. Durch die Nutzung von Software-Tools wie R, Python, Stata, SPSS und JASP kann der Q-Q-Plot effizient zur Datenanalyse eingesetzt werden.