Die Annahmen der linearen Regression: Voraussetzungen der Regressionsanalyse

Die lineare Regression unterliegt diversen Annahmen. Sind diese Voraussetzungen nicht erfüllt, so wirkt sich dies auf die Güte der Schätzung, wie auch die Ergebnisse der Tests in der Regressionsanalyse aus. Hierbei nimmt die Störgröße des Modells eine zentrale Rolle ein.

Bei den Modellannahmen handelt es sich um Linearität, Erwartungswert der Störgrößen beträgt Null, die Fehlerterme sind homoskedastisch, die Störgrößen sind nicht autokorreliert, es liegt keine Multikollinearität vor und die Fehler sind normalverteilt.

Annahme 1 der Regresssionsanalyse: Linearität

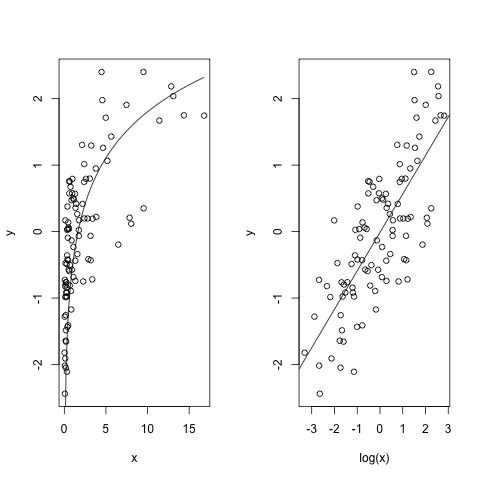
In dem Bild links sehen wir, dass der Zusammenhang zwischen x und y nichtlinear ist. Der Zusammenhang lässt sich gut durch eine Kurve, jedoch nicht durch eine Gerade erklären. Wird x mittels des Logarithmus transformiert, so ist der Zusammenhang zwischen log(x) und y linear. Dies sehen wir im Bild rechts. Wird eine solche Nichtlinearität nicht entdeckt und die untransformierte Variable in der Regression verwendet, so ist die Folge, dass die geschätzten Koeffizienten im Modell verzerrt sind. Verzerrt heißt, dass die geschätzten Koeffizienten für wachsende Stichproben nicht gegen den wahren Koeffizienten streben. Je nach beobachteten nichtlinearen Zusammenhang bieten sich verschiedene Transformationen an. Gängig sind dabei Transformationen mit der Exponetialfunktion, dem Logarithmus, der Quadratwurzel und beliebige Potenzen.

Kommende Grafik zeigt ein weiteres Phänomen, welches bei der Modellierung einer Regression auftreten kann.

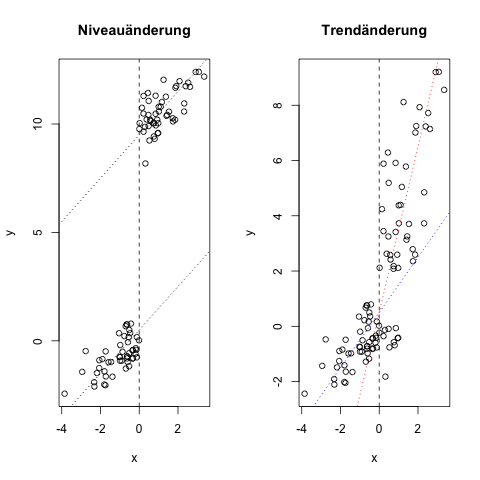
Wir sehen hier zwei Beispiele für eeinen Strukturbruch in unseren Daten. Strukturbrüche liegen häufig bei Zeitreihendaten vor. Im linken Bild erkennen wir, dass ab dem Wert x = 0, ein "Sprung" um 10 Einheiten vorliegt. Die Steigung beider Punktwolken ist gleich, jedoch unterscheidet sich der Achsenabschnitt. Im rechten Bild wird die Steigung zum Strukturbrucht stärker.

Solche Strukturbüche lassen sich in einem Regressionsmodell durch Dummy-Variablen berücksichtigen. Dabei nehmen diese Dummies den Wert 0 vor dem Strukturbruch und den Wert 1 (links) oder größer (rechts) nach dem Strukturbruch an.

Weiterhin kann eine Form der Nichtlinearität aufreten, in dem sich die Wirkung mehrerer unabhängiger Variablen nicht-additiv verknüpfen. Beispielsweise kann sich der Zusammenhang zwischen einer Variablen x und y bezüglich einer weiteren Variablen (zum Beispiel dem Geschlecht) unterscheiden. Wir sprechen hier von Interaktion. Mittels Interaktion lassen sich Moderatoreneffekte untersuchen. Dabie ist eine Interaktion mathematisch das Produkt aus zwei unabhängigen Variablen.

Annahme 2 der Regressionsanalyse: Erwartungswert der Störgößen ist gleich Null

Falls alle systematischen Einflussgrößen im Modell berücksichtigt wurden, so umfasst die Störgröße des Modells nur zufällige Effekte. Diese weichen positiv und negativ zwischen den beobachteten und geschätzten Werten ab. Dabei unterstellt das Regressionsmodell, dass die Fehler Erwartungswert Null besitzen. Diese Schwankungen sollen sich im Mittel als ausgleichen.

Eine Verletzung kan sich in der Praxis ergeben, wenn die Werte von y mit einem konstanten Fehler zu hoch oder zu niedrig gemessen werden. Hier wird von systematischen Meßfehlern und damit systematischen Effekten in der Störgröße gesprochen. Die kleinste Quadrate Schätzung der Regression erzwingt dabei das die Residuen den Wert Null aufweisen. Im Falle eines systematischen Meßfehlers geht dieser in den Wert des Achsenabschnitts des Modells ein. Somit wird dieser nicht mehr unverzerrt geschätzt. In dem meisten Anwendungen ist dies jedoch unproblematisch, da der geschätzte Achsenabschnitt von keinem Interesse ist.

Im Falle einer Regression ohne Konstante geht der systematische Meßfehler jedoch in die übrigen Koeffienten über, sodass jene verzerrt sind. Im Allgemeinen sollte eine Regression durch den Ursprung (also ohne Achsenabschnitt) inhaltlich gut begründet sein.

Annahme 3: Homoskedastizität

Eine weitere Modellprämisse verlangt, dass die Störgrößen gleiche Varianzen ausfweisen. Wir sprechen in diesem Fall von Homoskedastizität. Bei einer Verletzung dieser Annahme wird von Heteroskedastizität gesprochen. In der Situation von Heteroskedastizität sind die Schätzungen ineffizient und die Standardfehler verfälscht. Durch die Verfälschung der Standardfehler werden auch die Konfidenzintervalle ungenau.

Zur Aufdeckung von Heterosekdastizität ist zunächst eine visuelle Inspektion nütztlich. Hierbei werden die geschätzten Werte der Regression gegen der Residuen in einem Streudiagramm abgetragen. Kommende Grafik zeigt Beispiele für homo- und heterosekdastische Fehlerterme.

Das obere Bild zeigt eine Punktwolke mit einer annähernd konstanten Streuung. Dies ist ein Beispiel für Homoskedastizität. Weiterhin zeigt das untere Bild einer Punktwolke bei welcher die Streuung von links nach rechts größer wird. Dies ist ein klassisches Beispiel für heteroskedastische Fehler. Weiterhin existieren in der Anwendung ebenso statistische Tests, die auf Heteroskedastizität prüfen. Hierbei handelt es sich unter Anderem um den Breusch-Pagan- und den Goldfeld-Qunadt-Test. Liefern die Tests signifikante Ergebnisse, so spricht dies für heteroskedastische Fehler und eine Verletuzunng der Annahmme.

Wie oben erwähnt wirkt sich Heteroskedastizität sich auf die Standardfehler aus. Ausweg aus einem Heteroskedastizitätsproblem bieten dabei sogenannte heteroskestatizitätskonsistente Schätzer. Hierei werden die Standardfehler des Modells mittels sogenannter Sandwich-Schätzer ermittelt. Diese Sandwich-Schätzer sind dabei nicht für Heteroskedastizität anfällig. Alternativ können auch Transformationen der abhängigen Variablen das Problem der Heteroskedastizität eindämmen.

Annahme 4: Keine Autokorrelation

Die lineare Regression basiert auf der Annahme, dass die Fehlerterme unkorreliert sind. Im Falle von korrelierten Fehlertermen sprechen wir von Autokorrelation. Autokorrelation tritt vor allem bei Zeitreihen auf. Im Falle von Autokorrelation sind die Abweichungen der geschätzen Werte von den tatsächlichen Beobachtungen nicht mehr zufällig.

Autokorrelation wirkt sich wie Heteroskedastizität auf die Standardfehler aus. Wie im Falle von Heteroskedastizität kann Autokorrelation visuell inspeziert werden. Auch dies geht mittels der Residualplots.

Inferenzstatistisch kann Autokorrelation mittels des Ddurbin-Watson-Tests überprüft werden. Liefert dieser ein signifikantes Ergebnis, so spricht dies für Autokorrelation. Ebenfalls kann an Hand der Teststatistik die Art der Autokorrelation ermittelt werden. Die Teststatistik des Durbin-Watson-Tests kann Werte zwischen 0 und 4 annehmen. Ein Wert von 2 spricht für Unkorreliertheit der Residuen. Ist die Teststatistik kleiner als 2, so deutet dies auf negative Autokorrelation hin. Ist sie hingegen größer 2 so spricht dies für eine positive Autokorrelation.

Die 5. der Voraussetzungen: Multikollinearität

Die kleinste Quadrate Schätzung liefert im Falle einer exakten linearen Abhängigkeit zwischen Regressoren keine Lösung. Lineare Abhängigkeit bedeutet, dass sich ein Regressoren nicht als lineare Funktion aus den übrigen Regressoren darstellen lassen darf. In diesem Fall liegt perfekte Multikollinearität vor. Jedoch tritt perfekte Multikollinearität in der Praxis eher seltener auf. Im Falle von perfekter Multikollinearität liegt in den unabhängigen Variablen datenanalytisch die selbe Information vor.

In der Anwendung liegt jedoch immer ein gewisser grad an Multkollinearität vor. Der kleinste Quadrate Schätzer ist zwar unter Multikollinearität nach wie vor der linear erwartungstreue Schätzer mit der kleinsten Varianz, jedoch werden die Schätzungen mit steigender Multikollinearität unzuverlässiger.

In der Situation von Multikollinearität überschneiden sich die Streuungen der Variablen. Dies lässt sich durch kommende Grafik visualisieren. Die Multikollinearität kommt hierbei durch die geschwärzte Fläche in den Venn-Diagrammen zum Ausdruck. Durch diese Überschneidungen ist die kleinste Quadrate Methode nicht mehr in der Lage den Effekt einer Variablen richtig zuzuordnen.

Einen ersten Anhaltspunkt zur Aufdeckung bzw. Prüfung der Stärke der Multikollinearität liefert eine Korrelationsanalyse. Hohe Korrelationen nahe 1 oder -1 deuten dabei auf ernsthafte Multikollinearitätsprobleme hin. Jedoch misst die Korrelation nur paarweise Abhängigkeiten. Es kann somit trotz niedriger Korrelationen, starke Multikollinearität auftreten.

Um komplexere Abhängigkeiten zwischen einem und mehreren Regressoren nachweisen zu können, dienen die sogenannten Varianzinflationsfaktoren (VIF). Dabei wird für jede unabhängige Variable ein VIF berechnet. Als Faustregel gilt, dass die VIF nicht größer 10 sein sollten. Andernfalls geht von dem entsprechenden Regressor ein Multikollinearitätsproblem aus.

Ein Ausweg aus dem Multikollionearitätsproblem kann eine Erhöhung des Stichprobenumfangs sein. Dies ist jedoch häufig inpraktikabel. Weiter ist es Möglich mit Transfromationenen der Variablen zu arbeiten, aus den multikollinearitätserzeugenden Variablen neue inhaltlich sinvolle Variablen zu bilden oder die Durchführung einer Ridge-Regression.

Annahme 6: Normalverteilung der Störterme

Die Annahme normalverteilter Störgrößen ist für die Durchführung von Tests im linearen Modell relevant. Die Annahme kann mittels grafischen Hilfsmitteln überprüft werden. Nützlich ist in diesem Kontext vor allem das Quantil-Quantil-Plot. Hierbei werden die Quantile der Normalverteilung gegen die Quantile der Residuen in einem Sstreudiagramm abgetragen. Die Idee dahinter ist, dass wenn die Residuen einer Normalverteilung entstammen ebenfalls die Quantile der Residuen mit den Quantilen einer Normalverteilung übereinstimmen. Dies äußert sich in dem Diagramm in einer Punktwolke, deren Punkte sich anähernd auf einer Linie verteilen. Weiterhin liegt mit dem Shapiro-Wilk-Test ein Test auf Normalverteilung vor. In praktischen Anwendungen ist jedoch die grafische Inspektion auf Normalverteilung vorzuziehen.

Fazit: Annahmen/Voraussetzungen der linearen Regression

Die lineare Regression ist ein fundamentales Werkzeug der statistischen Analyse, dessen Aussagekraft und Zuverlässigkeit stark von der Erfüllung spezifischer Modellannahmen abhängt. Diese Annahmen stellen sicher, dass die Schätzungen der Koeffizienten präzise und die inferenzstatistischen Tests valide sind. Wird auch nur eine dieser Voraussetzungen verletzt, so hat dies nicht nur Auswirkungen auf die Güte der Schätzungen, sondern auch auf die Ergebnisse der statistischen Tests.

Eine der grundlegendsten Annahmen ist die Linearität, welche fordert, dass die Beziehung zwischen den erklärenden Variablen und der abhängigen Variablen in den Parametern linear ist. Werden nicht-lineare Zusammenhänge nicht erkannt und entsprechend transformiert, führt dies zu verzerrten Schätzungen, die nicht gegen den wahren Wert konvergieren. Ein weiteres Problem, das bei Zeitreihendaten auftreten kann, sind Strukturbrüche, welche mittels Dummy-Variablen berücksichtigt werden können.

Die Unverzerrtheit der Störgrößen ist eine weitere zentrale Annahme. Ist der Erwartungswert der Fehlerterme ungleich Null, etwa aufgrund systematischer Messfehler, so beeinflusst dies insbesondere den Achsenabschnitt des Modells. Zwar spielt dieser Achsenabschnitt in vielen Anwendungen eine untergeordnete Rolle, doch können in speziellen Modellen ohne Achsenabschnitt auch die Schätzungen der übrigen Koeffizienten verzerrt werden.

Ebenso wichtig ist die Homoskedastizität, die voraussetzt, dass die Varianz der Störgrößen konstant ist. Liegt eine Heteroskedastizität vor, führt dies zu ineffizienten Schätzungen und verfälschten Standardfehlern, was die Konfidenzintervalle und Hypothesentests beeinträchtigt. Heteroskedastizitätskonsistente Schätzer oder Transformationen der abhängigen Variablen bieten hier eine Lösung.

Die Annahme der Unkorreliertheit der Fehlerterme (keine Autokorrelation) ist vor allem bei Zeitreihendaten von Bedeutung. Autokorrelation, sei es positiv oder negativ, verfälscht ebenfalls die Standardfehler und beeinträchtigt die Zuverlässigkeit der inferenzstatistischen Tests. Tests wie der Durbin-Watson-Test helfen dabei, Autokorrelation zu erkennen und gegebenenfalls Gegenmaßnahmen zu ergreifen.

Ein weiteres potenzielles Problem ist die Multikollinearität zwischen den Regressoren. Zwar führt sie in der Regel nicht zu verzerrten Schätzungen, kann jedoch die Stabilität und Interpretierbarkeit der Koeffizienten erheblich beeinträchtigen. Eine hohe Multikollinearität erhöht die Varianz der Schätzungen und erschwert die Bestimmung des individuellen Einflusses der unabhängigen Variablen auf die abhängige Variable. Methoden wie die Berechnung von Varianzinflationsfaktoren (VIF) helfen, das Ausmaß der Multikollinearität zu bestimmen, und in einigen Fällen können Transformationen oder die Anwendung von Ridge-Regression Abhilfe schaffen.

Schließlich ist die Normalverteilung der Störgrößen besonders für die Durchführung von Hypothesentests entscheidend. Diese Annahme lässt sich durch grafische Methoden wie Quantil-Quantil-Plots oder durch den Shapiro-Wilk-Test überprüfen. Während für die Schätzung der Koeffizienten selbst diese Annahme nicht zwingend erforderlich ist, beeinflusst sie die Validität der inferenzstatistischen Schlussfolgerungen.

Zusammenfassend lässt sich festhalten, dass die lineare Regression ein mächtiges Werkzeug ist, dessen Ergebnisse jedoch nur dann aussagekräftig sind, wenn die zugrundeliegenden Annahmen erfüllt sind. Die Verletzung einer oder mehrerer dieser Annahmen führt zu Verzerrungen, ineffizienten Schätzungen oder falsch interpretierten Testergebnissen. Es ist daher entscheidend, die Modellannahmen sorgfältig zu prüfen und, wenn notwendig, geeignete Anpassungen vorzunehmen, um valide und belastbare Ergebnisse zu erhalten.